Chemical Wonders: Experimental Techniques (Part 4) - Nuclear Magnetic Resonance

Nuclear Magnetic Resonance Spectroscopy

Note: Assumed knowledge or previous experience with NMR in High School or University. 

This is perhaps one of the most important tools of chemistry, which involves an analyte absorbing energies from radiofrequencies. In particular, the absorption of radiofrequencies, is affected by the magnetic environment of the atomic nuclei in compounds. Thus it allows us to deduce structural information on the compound in question. It is typically used to determine the relative chemical environments of active atomic nuclei present in a compound, usually we analyse a solution of our analyte. Using a solution, we are also able to investigate the chemical behavior of the analyte.

We can take advantage of many different types of spectra depending on the atomic nuclei we want to analyse in a compound, the most commonly recorded spectra belongs to the Carbon-13 nuclei, in ¹³C NMR, usually used by organic chemists.

Suitable Nuclei

The three isotopes of hydrogen each have their own nuclei, which give their own NMR spectra.
From left: Hydrogen, Deuterium and Tritium. Wikimedia source. 

All nuclei have a property called "nuclear spin," a quantized property which is described by the spin quantum number, I, with the corresponding numbers 0, 1/2, 1, 3/2, 5/2 and so on. When nuclei aren't exposed to a magnetic field, the spin states are considered degenerate, i.e. the spin states have all the same energy. Conversely, when a magnetic field is applied to a nuclei, it becomes "split," i.e. it becomes non-degenerate, and the spin states have different energy levels. Nuclei where the value of I, is equal to 0, they are said to be NMR inactive. On the other hand, for nuclei where  I = 1/2, the nuclei is said to be NMR active, examples include ¹H and ¹²C nuclei.  

The ¹³C NMR spectra is important, because the carbon-13 isotope has a relative natural abundance of 1.1 %, so when investigating a compound, only 1% of all carbon atoms present in the compound will be the isotope. As a result, the relationship between  ¹H - ¹³C coupling has a consequence on the observed NMR spectra.

Given all of this, what constitutes a suitable nuclei? And what are some important factors that determine when an NMR spectra will be observed?

• The nuclear spin quantum number needs to be I ≥ 1/2;
• In general, it is advantageous for the particular nucleus to be in relative abundance, the ¹³C  isotope is one exception, though. Abundance of a particular isotope (isotopic enrichment) can be utilized to enhance the signal : noise ratios;
• The nucleus must posses a relatively short spin-relaxation time (T₁, given in seconds), which is dependent on the properties of the molecular environment and the nucleus itself;
• Finally, if I > 1/2, it results in a  non-spherical distribution of nuclear charge, which is termed a quadrupole moment. This leads to relatively short values and causes the signals associated with the quadrupole moment to appear broad; signal broadening is also observed on nuclei attached to the nuclei that possesses a quadrupole moment. For example, ¹¹B as well as an ¹H NMR spectra of protons attached to ¹¹B. 

The importance of the T₁  value becomes apparent when observing elements that have more than one NMR active form, for example ⁶Li and ⁷Li are both NMR active, but their values are different. Typically, ⁷Li has T₁ < 3 s, while for  ⁶Li is T₁ ≈ 10 to 80 s. Considering the relative abundance of these isotopes, we find that ⁷Li has an abundance of 92.5%, which makes it more suitable than ⁶Li .

Chemical Shifts and Resonance Frequencies

You can read a table of frequencies at which you would be able to observe certain nuclei using NMR here. NMR spectrometers are calibrated to particular resonance frequencies which are specific to a nucleus (e.g. ¹H, ¹³C, ¹¹B, ³⁵Cl, ³⁷Cl absorb different radiofrequencies), for example a 400 MHz spectrometer set to 400 MHz, you will only be able to observe ¹H nuclei; using the same 400 MHz spectrometer, but calibrated to 162 MHz, you would only be able to observe ³¹P. 

¹H NMR experiments involve identifying protons that are in different chemical environments (i.e. a H is bonded to different groups/atoms), which resonate at different frequencies.

For example, the proton NMR spectra of benzene (C6H6) only appears to have
one peak. Why? Every ¹H nuclei is bonded to the same 'environment' of a
C=C bonded to another proton.

The same is true for other types of NMR, which each give their own characteristic signals. Signals in an NMR spectrum are given a chemical shift value, 𝛿, which is relative to the specific radiofrequency of that nuclei. The chemical shift value is a parameter that is independent from the magnetic field applied to the analyte. It can be defined as:

𝛿 = (v - v₀) / v₀ =  Δv / v₀

The value of 𝛿 is usually quite small and inconvenient, so we usually multiply by 10⁶, converting it into ppm (parts per million). The IUPAC convention for 𝛿, according to their Gold Book is defined as:

𝛿 = (v - v₀) in Hz / v₀  in MHz

For  ¹H and ¹³C NMR, the standard reference is tetramethylsilane, SiMe4. It is used as a reference for the shift, so to speak, of the signals from a particular nuclei from the reference signal. A positive 𝛿 is a shift to a higher frequency, while a negative shift (or less positive), means there is a shift to a lower frequency. This difference is the chemical shift. 

Homonuclear spin-spin coupling

A nucleus can only occupy two spin states (-1/2 and +1/2), the energy difference between these spin states is dependent on the magnetic field produced by the NMR spectrometer. If say, there is a system where there are two magnetically non-equivalent ¹H nuclei, there can only be situations (H_A and H_B) that can arise when a magnetic field is applied:

• The NMR signal for H_A is split into two equal lines when a magnetic field is applied to H_B, these equal lines are also produced by H_B. The lines produced by are dependent on the which spin state of is "seen" by the spectrometer. These protons are said have coupled, producing two "doublets." The coupling constant, J, which is measured in Hz is defined as the splitting that occurs between two lines in each doublet. 
• When no coupling of nuclei occurs. The local magnetic field produced by the spin of results in two resonances, each of these a singlet, as no coupling has occurred between the two nuclei.

Heteronuclear spin-spin coupling

Statistically, the ¹³C nuclei is quite rare.  So in ¹H NMR of say, acetone and assuming a natural distribution of carbon isotopes, you will not be able to observe the coupling of  ¹H - ¹³C. Conversely, You will observe this coupling when using ¹³C NMR spectrum on acetone, and will only observe a singlet because of the C=O group, and a quartet because of the two chemically equivalent -CH3 groups. You can see this in this spectra here.

Ion-solution exchanges can be observed using NMR

The exchange of cations into solution occurs at slow enough speeds to be observed at the NMR spectroscopic timescale. We utilize the ¹⁷O isotope as a label: because it is NMR active, and because I = 5/2. From the signal ratio of  ¹⁷O present in a naturally isotopic distribution of co-ordinated water (recall H₂O can form weak bonds with ions), you can actually find the hydration value of a given ion-water complex. For example, the Cu2+ ion has been found to co-ordinate (bond) with six water molecules, forming the complex ion [Cu(OH₂)]²⁺ (hexaaquacopper(II)), forming an octahedral complex. See model below:

Hexaaquacopper(II), has six water molecules whose
hydration number using  ¹⁷O can be observed.

Another exchange process are redistribution reactions, in which, substituents (chemical groups) are exchanged between chemical species - but - the types of bonds and number of bonds remain. Similar to a substitution reaction. For example, the reaction of Triethyl phosphite and Phosphorus trichloride:

PCl₃  +  P(OEt)₃   ⇌  PCl₂(OEt)  +  PCl(OEt)₂

We can find were the equilibrium lies using ³¹P spectroscopy, and the rate data by analysing the variation in the signal integrals (peaks), conversely, you can find the equilibrium constant (Kc) when no more variation is found in  the signal integrals. Finding the equilibrium will allow you to find the all-important free energy change of the system (ΔG^o = -RT ln K). Using this relationship you can then find the at varying temperatures using ΔG^o =  ΔH^o - TΔS^o. Thus, we can find the equilibrium position can be found in relation to temperature (remembering that ΔH^o is almost 0, using the second law of thermodynamics), we can then differentiate to eventually find:

d ln K / dT  =  ΔH^o/RT²

I won't go into how NMR machines work, but here's what they look like:

A Bruker NMR spectrometer connected
to a computer. Wikimedia link.

A high-powered NMR machine from Varian, capable of
using 900 MHz frequencies. 

Further Reading/ Useful links:

• http://www.chemguide.co.uk/analysis/nmr/interpretc13.html
• https://www2.chemistry.msu.edu/faculty/reusch/virttxtjml/spectrpy/nmr/nmr1.htm
• https://www.ucl.ac.uk/nmr/NMR_lecture_notes/L3_3_97_web.pdf
• http://users.wfu.edu/ylwong/chem/nmr/h1/

                                                                                      

Unwinding the Double Helix: The Structure and Function of Nucleic Acids (Part 3)

The Function of Nucleic Acids

                                                                                 

So far, I've only discussed the main structures of nucleic acids - the primary, secondary and tertiary structures. This section will focus on the function nucleic acids in cells and the denaturation of nucleic acids.

Genetic Biochemistry - from genes to proteins

In my blogs I haven't quit covered the biochemistry of genetics in detail, so think of this part as a (very) brief overview of molecular genetics. It's important to remember that the main function of nucleic acids is to store genetic information and that they are the key to biochemical processes, namely, protein synthesis. 

What's in a genome?

All living things carry genes - sections of DNA which, when 'read' by your molecular machinery, result in the expression of a particular gene. Expression leads to the synthesis of a chemical, usually a protein of some description, such as an enzyme. Depending on the organism, their genetic information can be stored as double-stranded DNA or RNA molecules which can vary in length. Genomes are also present in viruses (which aren't considered 'alive'), which generally contain a few thousand bases (b) that code for the proteins that make up the viral structure.

The E. coli bacteria had its circular genome sequenced in 1997, which contains about 4.64 million base pairs (1.6 mm in theoretical length), all of code for about 4000 genes, 50 of which are considered 'non-essential'.  Another bacteria, the pathogenic Clostridium difficile has about 4.4 million base pairs. An interesting thing to not about these bacteria is that, even though they contain less genetic material than us, they have a higher gene density than us.

Comparatively, the human genome was sequenced in 2001, we found out that it contains about 3.0 ×10⁹  base pairs (3,200 Mb, megabase pairs). The full sequencing and analysis of our genome revealed that:

 There appear to be about 30,000–40,000 protein-coding genes in the human genome—only about twice as many as in worm or fly. 

This came as a surprise to many who had thought that we were more complex than other organisms, and the fact that only 1.33x10-5 % of our genome codes for essential proteins. Much of our genome has been termed as 'junk DNA.'  It is possible that this junk, referred to as non-coding DNA (ncDNA), is essential for regulation at the genetic level. I'll leave some links at the bottom of this post if you want to read more about this section of our DNA. 

Gene Expression: An overview

In most organisms it is those genes that are 'read,' synthesising RNA for use by ribosomes, and thus directing the synthesis of proteins. This process of gene to protein is called gene expression. 

Transcription: the first step of gene expression

The first step involves the DNA strand being unwound, by a leading enzyme. Behind it is RNA polymerase, along with other enzymes, which begins to 'read' the DNA strand, which becomes the template for the RNA being produced. It works in a similar fashion to DNA replication, but instead produces a single-stranded RNA molecule, called mRNA. This process is powered by ribonucleoside triphosphates, such as: ATP, GTP, CTP, and UTP, which are all needed to make RNA. Again, similar to to DNA replication, this process requires the use of a class of enzyme called polymerases. Specifically, the RNA polymerases. This process can be summarised below:

1) RNA polymerase bind to the promoter, which begins transcription

2) RNA polymerase goes along the DNA strand, opening up the strand "downstream," while the strand closes "upstream." A strand of RNA is produced which is complementary to the bases present on the template strand:

3) Once RNA polymerase reaches the termination "STOP" codon, it detaches from the DNA strand and a pre-mRNA strand is produced. This is then 'edited' by enzymes, removing non-essential regions called introns (I'm not going to cover this process here). 

Translation: proteins from mRNA

mRNA exits the nucleus of a eukaryotic cell via nuclear pores, it then comes into contact with a special protein called a ribosome. Ribosomes work together with strands of RNA called tRNA, which have 3 bases (a anti-codon) which are complementary to the codons present in mRNA. tRNAs basically are your cell's code-cracking sheets, as they are attached to the amino acid which correspond to the mRNA codon. The ribosome is effectively the machinery that sticks together the amino acids on the tRNA, eventually creating a protein. Proteins aren't usually folded by themselves, and often require assistance via a molecular "chaperone," a family of proteins called chaperonins. There are 64 combinations of codons, all of which correspond to an amino acid, found on tRNA. Here is a table:

Nucleic Acid Denaturation

As mentioned previously, DNA and RNA is incredibly stable - however, because of the need to replicate DNA for meiosis and mitotic cell division, the secondary structure must not be too stable. If DNA and RNA where to be too stable, replication and gene expression rely on the uncoiling, and recoiling of double-stranded nucleic acids. Physiological conditions (~pH = 7, 298.15 K (25 ℃), 1 atm) allow cells to be opened up by the required enzymes in vivo.

But what happens if a nucleic acid's secondary structure opens up too much? If the secondary structure is lost, it is called denaturation. Separating strands, like all things in chemistry, obey thermodynamic laws, in this case the free energy change:

ΔG = ΔH - TΔS                (helix ⮂ random coil)

The secondary structure is stabilised by phosphodiester bonds, hydrogen bonds and base stacking, as mentioned in the previous sections. These interactions contribute to the heat of a nucleic acid system, i.e. they are enthalpic, so ΔH in the equation above will be positive. And since helices are very ordered, the entropy change, once denatured, will result in a positive ΔS.  

Low temperatures result in a lower ΔG, because the - TΔS  portion of the equation is positive, due to a reduction in randomness because of a lower temperature. This results in a ΔG > 0, meaning the helix is relatively more stable than at higher temperature. As such, when the temperature increases, - TΔS becomes greater than the ΔH value, resulting in ΔG < 0, which decreases the stability of the helix, eventually the double helix falls apart. It is possible that slowly cooling can reverse this process.

Denaturation of nucleic acids can actually be observed through a spectrometer set at the ultra-violet range (260 nm) when slowly heating a solution of DNA. When doing this, you would notice that the absorbance of the solution increases over time as the purine and pyrimidine structures become more "free." This happens because the structure of DNA, where nucleotides are packed in tightly in a double helix results in a decrease in light absorption, a process called hypochromism.

                                                                                                                                      

Futher reading on 'Junk-DNA' :

• https://www.abebooks.com/9780231170840/Junk-DNA-Journey-Dark-Matter-023117084X/plp
• http://www.pnas.org/content/111/17/6131
• https://books.google.co.nz/books/about/Non_coding_RNAs_and_Epigenetic_Regulatio.html
  

                                                                                                   

As always, thanks for reading!

Don't forget to check out my Patreon,  if you like the content I'm putting out:

 https://www.patreon.com/MrElement 

Links provided bring you to some of the info I used, the first year university textbook, "Biochemistry: Concepts and Connections," 1ED, by D.R. Appling, Pearson Ed. LTD. Chapter 4: Nucleic Acids, pgs 126-129, was used as a guide to write this post. You can buy it here.

I also used the textbook, "Molecular Biology," 5ED, by Weaver, Robert F., McGraw HIll Publishing; which if you're interested (and have the money to spare). Chapter 3: An Introduction to Gene Function, pgs 31-45, was used as a guide to write this post. You can buy it here.

Unwinding the Double Helix: The Structure and Function of Nucleic Acids (Part 2)

The Three-Dimensional Structure of Nucleic Acids 

Nucleic acids, as with any molecule, possess a three-dimensional structure. Nucleic acids can be described into three main levels of structure: the primary, secondary, and tertiary structure. By describing these, we start to unravel why nucleic acids behave the way they do - and why they are capable of being the genetic material found in all forms of life and phages.

The Primary Structure of nucleic acids

In the diagram above you can see that : the polynucleotide chain has a sense (directionality), where you 'read' it in the direction of the phosphodiester linkage between the 3' carbon of one monomer, to the 5' carbon of the next. The result is the nucleic acid carries an unreacted phosphate (P_i) group on the 5' end, and an unreacted 3' hydroxyl, the 5' to 3' logic is used to 'read' nucleic acids by ribosomes and other proteins involved with nucleic acid synthesis, replication etc. And as is the nature of nucleic acids, they each have a specific nucleotide sequence and for any one nucleic acid, this sequence is its primary structure.

When describing a polynucleotide, it is awkward and quite unnecessary to draw out the entire sequence of nucleotides, the diagram becomes cumbersome. There are several ways of representing the primary structure. For example, if you just want to represent the base sequence, you can do so like this (the first 40 nucleobases of human insulin, on chromosome 11) :

5'  ~[... AGCCCTCCAG GACAGGCTGC ATCAGAAGAG GCCATCAAGC ...]~  3'

In between each letter is a phosphodiester bond, all of these can be assumed to bond to be from a 3' hydroxyl to a 5' phosphate on the next nucleotide. Where the primary sequence ends with a 3',  is where the unreacted hydroxyl group is located; conversely, the 5' end is where the unreacted phosphate group occurs.

Hydrogen bonds and helices - the secondary & tertiary structure

The amazing helical shape that nucleic acids can form is familiar with most, it and similar structures occur due to the nucleobases interacting in respect to one another - this interaction results in the secondary structure. Some examples include the tRNA molecule and the double helix found in DNA. The secondary structure of DNA can vary in many forms (conformations) notably the A,B and Z forms. The majority of DNA adopts the B-DNA form, on the other hand, double-stranded RNA and DNA-RNA hybrids usually adopt the A conformation. These forms can occur due to changes in the chemical environment of the cell (including hydration level). You can see them below:

The tertiary structure on the other hand occurs only because of 'longer-range' interactions in the secondary structure. The best example of this occurs when DNA supercoils, compacting it and allowing the large molecule to fit inside cells and phage particles. Supercoiling is present in circular DNA and linear DNA. To understand how supercoiling works, first consider a B-DNA molecule that is a base pairs in length; B-DNA typically has 10.5 base pairs per helical turns. Now that we know this we can consider this B-DNA molecule completes y amount of turns, this number is what we call the Twist (T); if the circular DNA covalently joins at the last turn we say the molecule has a Linking number (L) of y. If this molecule. 

If we rotate this molecule counter-clockwise by one turn (360^o), it becomes strained (as this reduces the Twist of the helix making it less stable), causing the B-DNA molecule to have 11.67 base pairs per turn (bp/turn). If the strained B-DNA molecule is allowed to return to its more stable conformation, it writhes (W) into a helix with 10.5 bp/turn once again. We can define the writhe as being negatively supercoiled, as W will have a value of -1. If the B-DNA molecule is rotated by two turns, W will have a value of -2, and so on. Overwound DNA is the opposite of this, by rotating it clockwise one turn W will be +1, and so on.

The degree of coiling in supercoiled DNA can be defined by the superhelix density (𝛔), which equals the change in linking number (𝚫L) over the linking number of the relaxed structure (L₀), this relationship can be written as:

𝛔 = 𝚫L/L₀

 Coiling also occurs in single-stranded nucleic acids whether they are RNA or DNA. For example: 

• In denatured single strands there is considerable flexibility of nucleotides (residues), resulting in coils and no specific structure.
• Non-self-complementary single strands, such as mRNA create a "stacked-base" structure, where the nucleobases stack, pulling the polynucleotide chain into a non-hydrogen bonding helix. The stacked-base structure is the normal shape assumed by these types of nucleic acid structure under physiological conditions.
• Finally, the "hairpin" structure forms when single stranded nucleic acids are self-complementary. The strand folds back on itself, making a stem-loop structure, much like a hairpin. This can be seen in tRNA, an important molecule in gene expression. See below:

If you'be been reading my previous blogs, you would've noticed that the primary, secondary and tertiary structure of nucleic acids is somewhat analogous in definition to that of proteins. This is because both class of molecule share the same chemical principles when it comes to observing the structure of three-dimensional biological macromolecules. 

                                                                                                                             

Further reading:

• https://www.ncbi.nlm.nih.gov/books/NBK6545/ 
• https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2441783/ 

                                                                                                                              

As always, thanks for reading!

Don't forget to check out my Patreon,  if you like the content I'm putting out:

 https://www.patreon.com/MrElement 

Links provided bring you to some of the info I used, the first year university textbook, "Biochemistry: Concepts and Connections," 1ED, by D.R. Appling, Pearson Ed. LTD, was used as a guide to write this post. You can buy it here. 

Unwinding the Double Helix: The Structure and Function of Nucleic Acids (Part 1)

The Molecular Blueprints for Life

                                                                                                                                 

Depending on how long you've been following me for, you would know that I've already covered the basics of what DNA and RNA is, and how it works. In this series, we'll explore the what makes nucleic acids so special. For one, they are the only biological substance capable of self-replication thus enabling it to pass on information from one generation to the next. Inside this molecular code is information for everything that makes you, you - from the proteins that make your muscles, to the enzymes that allow you metabolise stuff. Mapped out and programmed, much of your development from child to adult, is coded within your very DNA. 

A Brief History of DNA

• During the Franco-Prussian war in 1989, the military scientist Friedric Miescher 'discovered' DNA when he was analyzing discarded surgical dressings, to which he found very small quantities of some sort of acid. In this analysis, this acid was found predominantly in the nuclei of white blood cells.  Aptly, he named this substance "nuclein".
• In the years 1884 to 1885, the scientists Oscar Hertwig, Albrecht von Kölliker, Eduard Strasburger, and August Weismann all provide evidence (independently) that the nucleus of a cell contain the information for inheritance.
• Four years later, in 1889, Richard Altmann renames Miescher's discovery as "nucleic acids" instead of nuclein. 
• By 1910, Thomas Hunt Morgan uses the Drosophila fruit fly to study inheritance, and discovers the white-eyed mutant. Three years later, with his colleague Alfred Sturtevant, they create the first genetic map for a chromosome in the Drosophila fruit fly. 
• Frederick Griffith, in 1928, discovered that when a non-virulent strain of bacterium (Streptococcus pneumoniae) are able to become virulent when mixed with heat-disabled virulent strains. He called this the "transforming principle."
• In 1929, Phoebus Levene discovers the building blocks of DNA.
• In 1942, George Beadle and Edward Tatum make the discovery that genes are responsible for the production of proteins.
• In 1944, Oswald T. Avery, Colin MacLeod, and Maclyn McCarty demonstrate that a discovery made in 1928 by Frederick Griffith is not the result of proteins being transferred between bacteria. Highly suggesting that nucleic acids are the genetic material. 
• From 1949 to 1950, Erwin Chargaff discovers that the base composition discovered by Phoebus Levene varies between species in different quantities. 
• Using the T2 bacteriophage, in 1952, Alfred Hershey and Martha Chase discover that it is the genetic material of virus, not the proteins that infect the bacterium. 
• By 1953, Rosalind Franklin used x-ray diffraction to produce high-resolution images of the DNA structure, suggesting that it has a double-helix shape. Later that year, Francis Crick and James Watson produce the first model of DNA - a double helix in which the bases A always pairs with T, and C with G. Their discovery was published in April 25 1953 in the magazine Nature.
• Matthew Meselson and Franklin Stahl discover how DNA replicates in 1958.
• From 1961 to 1966, Robert W. Holley, Har Gobind Khorana, Heinrich Matthaei, Marshall W. Nirenberg and their colleagues manage to figure out what some genes code for what amino acids. "Cracking" the genetic code. 
•  Paul Berg, in 1972 manages to create the first bit of recombinant DNA. By 1977, Frederick Sanger, Allan Maxam, and Walter Gilbert create the first method of sequencing DNA.
• In 1982, the first commercial application of DNA technology using recombinant DNA is produced - human insulin becomes widely available and much easier to produce. A year later, Kary Mullis discovers the polymerase chain reaction (PCR) as a way to produce many copies of DNA in vitro.
• After eight years, the sequencing of the human genome begins in 1990, which is only completed and then published 11 years later in 2001. The next year, the first genome of the model mammalian organism, the mouse, is completed.

The DNA molecule is recognised by everyone - the hallmark double helix structure is the go-to image for biosciences. With it, it has changed the way we think about the living world - it is the result of more than 100 years of hard work and dedication. Understanding DNA has lead us to develop new technologies to treat illnesses and hereditary diseases, and as demonstrated in 1982. The nature of how genes are passed on has been fundamental to modern agriculture and is responsible for the Green Revolution in the '30s to '60s and to now, where we are able to create hardier and more resilient crops than ever. You can check out my other blog series about Gene Editing here.

Two Types of Nucleic Acids

It is recognised that there are two types of nucleic acid: Miescher has discovered deoxyribonucleic acid (DNA), later it was discovered there was another type of nucleic acid, called ribonucleic acid (RNA). In each case, they are polymers - made of smaller molecules called monomers linked in a large chain. Their differences can be summarised below: 

Both RNA and DNA contain three main constituents which make up the nucleotides:

• A five carbon sugar, called ribose in RNA, and 2-deoxyribose in DNA. Their structure differs as below:
• A phosphate group, which forms a phosphodiester link between two sugar residues, forming the back bone of the nucleic acid. You can see how they look below:
• And finally, the nucleobases, which can be seen above and are bonded to the 1' carbon of the sugar. These bases form hydrogen bonds with the adjacent strand, and in the case of mRNA, pair with tRNA to enable protein production. They can be separated into two types: the purines (Adenine and Guanine) and the pyrimidines (Cytosine (and 5-methylcytosine) ,Thymine, and Uracil which is found RNA only). The chemical bond between the carbon 1' of the sugar and the nucleobase is termed as a glycosidic bond.

  

Nucleotides and their derivatives

As noted above, nucleotides are the monomers that make up the DNA strand and are connected via phosphodiester linkages. Nucleotides are considered to be the phosphorylated derivative of a nucleoside, which lack the phosphate group on the 5' carbon of the sugar group. Large stretches of nucleotides are often called polynucleotides while those with a few are termed oligonucleotides (dinucleotides, trinucleotides, tetranucleotides etc.).

Noted before as well, RNA contains the ribose sugar, in which the 2' OH group is still present, giving it a different function than with the DNA deoxyribose form. This is because the 2' OH group is found in RNA enzymes called ribozymes, which were discovered by Thomas Cech and Sidney Altmann independently. Because of this, many biochemists think that it is possible that RNA came into existence earlier than DNA. DNA is much more stable than RNA, which allows it to be much larger than its ribose counterpart. 

Nucleotides are strong acids where the ionization of the phosphate group and the deprotonation/protonation of the bases at pH values around 7. The nucleobases are also capable of converting into different tautomeric forms because of the several double bonds present in the ring structure (a form of conjugation). For example, uracil can convert between the keto and enol forms:

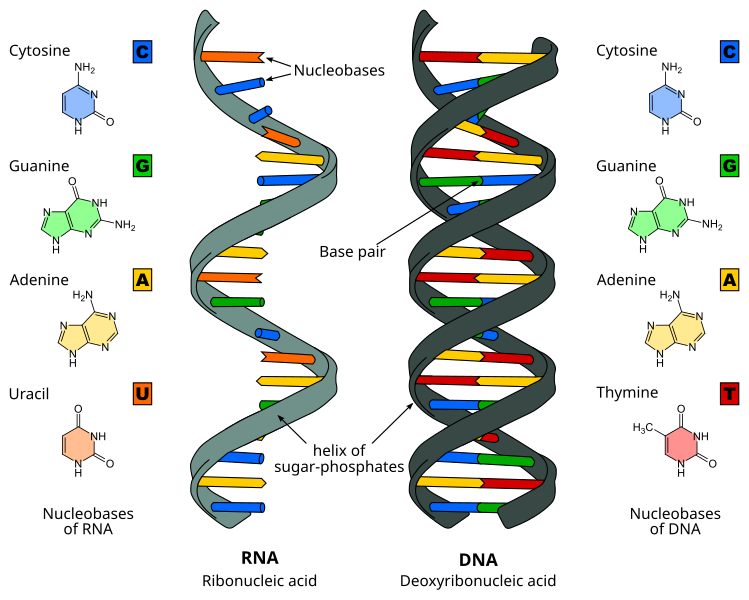
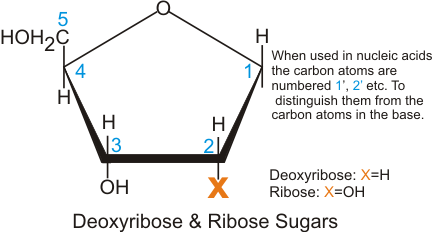
A consequence of highly conjugated chemical structures is how much the molecules absorb light. Purines, pyrimidines and their derivatives (nucleic acids, nucleotides and nucleosides) all absorb light in the ultraviolet region. You can scroll down on the papers here, and here to see these spectra. Normally we use these spectra to make quantitative measurements at the 260 nm setting on a spectrophotometer. 

Another important part of nucleotides are the phosphodiester bonds present in the DNA molecule. These bonds are formed by "adding" a water to the monomers. The opposite is true, hydrolysis removes a water molecule from this bond, releasing a ∆Gº' = +25 kJ/mol, as a result, this is a thermodynamically favoured reaction. See below to see how this looks like:

In the cell, both RNA and DNA are broken down by nucleases, catalysing reaction (2) above, generally this reaction is utilised in metabolic pathways as a way to create glucose, or ketone bodies to produce energy, excess nitrogen is converted into urea and then excreted (more on this in my Metabolism and the Energy of Life series). As discussed in that series, ATP is often used by the body to drive forward reactions that would otherwise be impossible in vivo. The polymerization of nucleotides is such a reaction, leading to the phosphodiester bond's stability.

In fact, DNA is so stable, it has been found in bones recovered to be as old as 80,000 years old. This assisted us in sequencing the complete genome of an extinct human species, the Neanderthal in 2010.  The resilience of DNA has also helped us map the genetic distribution of our own species, from Africa to beyond. A truly wonderful molecule!

                                                                                                               

Now that you've been acquainted with nucleic acids. the next section will go over its primary structure. 

As always, thanks for reading! 

Don't forget to check out my Patreon,  if you like the content I'm putting out:

 https://www.patreon.com/MrElement 

Links provided bring you to some of the info I used, the first year university textbook, "Biochemistry: Concepts and Connections," 1ED, by D.R. Appling, Pearson Ed. LTD, was used as a guide to write this post. You can buy it here. 

Your body's defense system: Antibodies (Part 3 of 3)

The above image is a colourised electron micrograph that of a T-cell  (green) infected by HIV H9 viruses (yellow) budding on the cellular surface. It would be beautiful, were it not so deadly.

                                                                                                                                

 Antibodies are used in an array of different defence situations

So far, I've only covered how your immune system produces antibodies that tag and aggregate an antigen (foreign substance) which is then consumed by a macrophage (white blood cell) in a process known as the humoral immune response. But there's the other form of defense too: the cellular immune response. As we've established previously, the cellular immune response involves a specific set of cells called lymphocytes that recognise and destroy foreign cells (antigens).

When people undergo transplants, it's commonplace that a few patients' bodies will undergo tissue rejection. The cellular immune response plays a role in this phenomenon as cells that don't quite match you own have different receptors on the cell surface, this leads to lymphocytes rejecting the donor's organ as those regions are recognised as an antigen. Your body also can utilise this system to destroy any potential cancer cells before they propagate to unmanageable quantities, this doesn't always work, though.

In both humoral and cellular immune responses have a similar molecular method of recognising foreign objects by using proteins belonging to the immunoglobulin superfamily. In the four examples below, if your eyes are good, you'll notice they all share similar sheet and loop structures. PDB IDs (protein database ID) are and links to their RCSB PDB profiles are listed:

Left: A class I human major histocompatibility complex (MHC), PDB ID: 1a1m; Right:  A class II human MHC, PDB ID: 1dlh

Left: A human T-cell receptor binding to a MHC class I molecule and a viral peptide; PDB ID: 1bd2; Right: A Murine F_ab  fragment; PDB ID: 1nca (the link shows for Fab fragments bound to a neuraminidase.

I'd definitely recommend checking out those RCSB links; they have 3D models of these molecules so you can have some idea of how they bind to antigens (some of the models include an antigen).

In the header and throughout this part I've mentioned T cells quite a lot. These cells are involved in the cellular immune response and have structures similar to the F_ab  fragments of antibodies on their cellular surface. Consequently, these cells target unwanted cells and are able to destroy them, which is why they have the name of Killer T cells ( or "cytotoxic T cells"). Receptors on the outside of these cells are capable of recognising foreign peptide chains on the surface of invading or infected cells. The examples shown above include MHC proteins, these are found on killer T cells and act as a switch that releases an attack protein called perforin. Perforins are released only when a T cell receptor (including the MHCs) detect an antigen, these then react with the detected invasive cell's membrane and form pores that effectively drain the cell of essential ions - killing the cell.

Why AIDS vaccines are so hard to produce based on what we've covered so far

Acquired Immune deficiency syndrome (AIDS) is a symptom of the problematic human immunodeficiency virus (HIV). HIV attacks T cells that are essential in a healthy immune system. The infected type of T cells that HIV infects are part of the first line of defence against antigens - they signal a set of B cells that produce important antibodies that help identify and destroy foreign objects. In effect, HIV completely disables the body's ability to defend itself.

To make matters worse, HIV undergoes mutations in it's genome (and therefore the antigenic determinants change often) at 60 times the rate of the influenza virus. Making a flu vaccine is problematic enough because the same reason - once we make a vaccine, and many viruses are destroyed, those remaining (somewhere in the human population) have already mutated and cannot be recognised by a complementary antibody.

So far we've only been able to slow the progress of AIDS, through therapies involving drugs that target the processes that replicate the viral genome in cells.

Here's hoping some brilliant person will figure out a way to stop the AIDS pandemic which has ruined 60 million lives since 1983.

                                                                                               

And that concludes this short three-part series! Make sure to look into more of this subject.