5 Apr 2017

Modelling Molecules: Molecular Orbital Theory (Part 1) - Bonding in Homonuclear Diatomic Molecules

What is Molecular Orbital (MO) theory?

Molecular orbital theory is an expansion on VSEPR theory (check the link if you need a referesher), which you should've learned about in High School. MO theory differs from VSEPR theory, in that it takes into account regions of space spread over the entire molecule in which you might find an electron. MO theory allows us to calculate these areas, called molecular orbitals, the nuclei of the atoms are placed in their equilibrium position for these calculations. Molecular orbitals form from interactions arising in the molecule, between the nuclei and the orbitals surrounding them. These interactions are restricted by several factors:

Interactions are allowed only if the symmetries of the atomic orbitals are compatible, i.e. they can 'fit' together;
The relative energies of the atomic orbitals is also very important, as the further apart in terms of energy each atomic orbital is, the less likely they will be to form a molecular orbital;
the region of overlap between atomic orbitals needs to be significant enough for a MO to form.

The amount of MOs that form always equals the amount of atomic orbitals present in the molecule. It's important to remember that all MOs have associated energies, so electrons will fill MOs according to the Aufbau principle. You can sum all the energies of the MOs to get the total energy of the molecule.
So what if we apply this so a very simple molecule, such as H₂?

MO Theory in H₂

Molecular orbitals are indicated by wavefunctions, 𝜓, which describe the nature of electrons within that orbital. Since electrons are also considered waves, the overall sign of the wavefunction can either be + or -. Additionally, just like waves, they can be described as transverse waves, i.e. they can interferre in a constructive (in-phase), described as "bonding" and destructive (out of phase), described as "anti-bonding" in MOs. We can describe these types of bonding orbitals as linear combinations of their respective atomic orbitals. The respective mathematical functions of these orbitals can be simplified as 𝜓MO(in-phase) and 𝜓*MO(out-of-phase), where N is a normalizing constant:

𝜓_MO(in-phase) = 𝜓_MO = N[𝜓₁ + 𝜓₂]

𝜓_MO(out-of-phase) = 𝜓*_MO = N[𝜓₁ - 𝜓₂]

N can be determined the equation below, whee S is the "overlap integral", a measure of how the regions of space:

N = 1 / √2(1+S) ≈ 1/√2

N* = 1 / √2(1-S) ≈ 1/√2

S is not taken into account in the approximate values given. The diagram above shows that the bonding MO, 𝜓_MO, is stabilized by the Is orbitals from the contributing H atoms, to form the bonding orbital. Conversely, the anti-bonding MO is destabilized, because the difference in energy between the anti-bonding MO and the 1s orbitals is slightly bigger than that between the bonding MO - this effect is far to complicated for me to explain in my blogs, it is however important to remember.
We can represent the anti-bonding and bonding orbitals in 3 dimensions, as anti-bonding orbitals form nodes due to destructive interference; the first orbital shown is the highest occupied molecular orbital, or HOMO for short, and the second is the lowest unoccupied molecular orbital, or LUMO. The HOMO is the bonding orbital as and the LUMO is the anti-bonding orbital:

You would notice that there is separate colours in the LUMO, indicating that there is a node in between and the 1s orbitals that make up the MO are out of phase.

Bonding in other X₂ type molecules

Now let's have a look at other molecules, say F2 and O2, which have 2s and 2p orbitals; recall from VSEPR theory that these orbitals have a maximum of 2 and 6 electrons each, respectively. The bond order can be calculated like this:

Bond Order = 1/2(total bonding electrons - total anti-bonding electrons)

We are only concerned with the valence shells, so we'll only display it as the 2s and 2p orbitals. The number of MOs equals the amount of atomic orbitals (as in VESPR), from this we can determine that the HOMO is 1/2 number of total valence electrons, LUMO on the other hand is the HOMO+1. Using the Aufbau principle, we can draw up a diagram as with Hydrogen, so we get (remember this is not starting at the 1s orbital):

Using chemistry software it is possible to model these MOs using quantum calculations, various types of these calculations exist with higher or lesser degrees of accuracy. The HOMO can be seen below:

Now let's try it with F2:

The HOMO will be MO9, and can be represented as:

Thanks for reading!
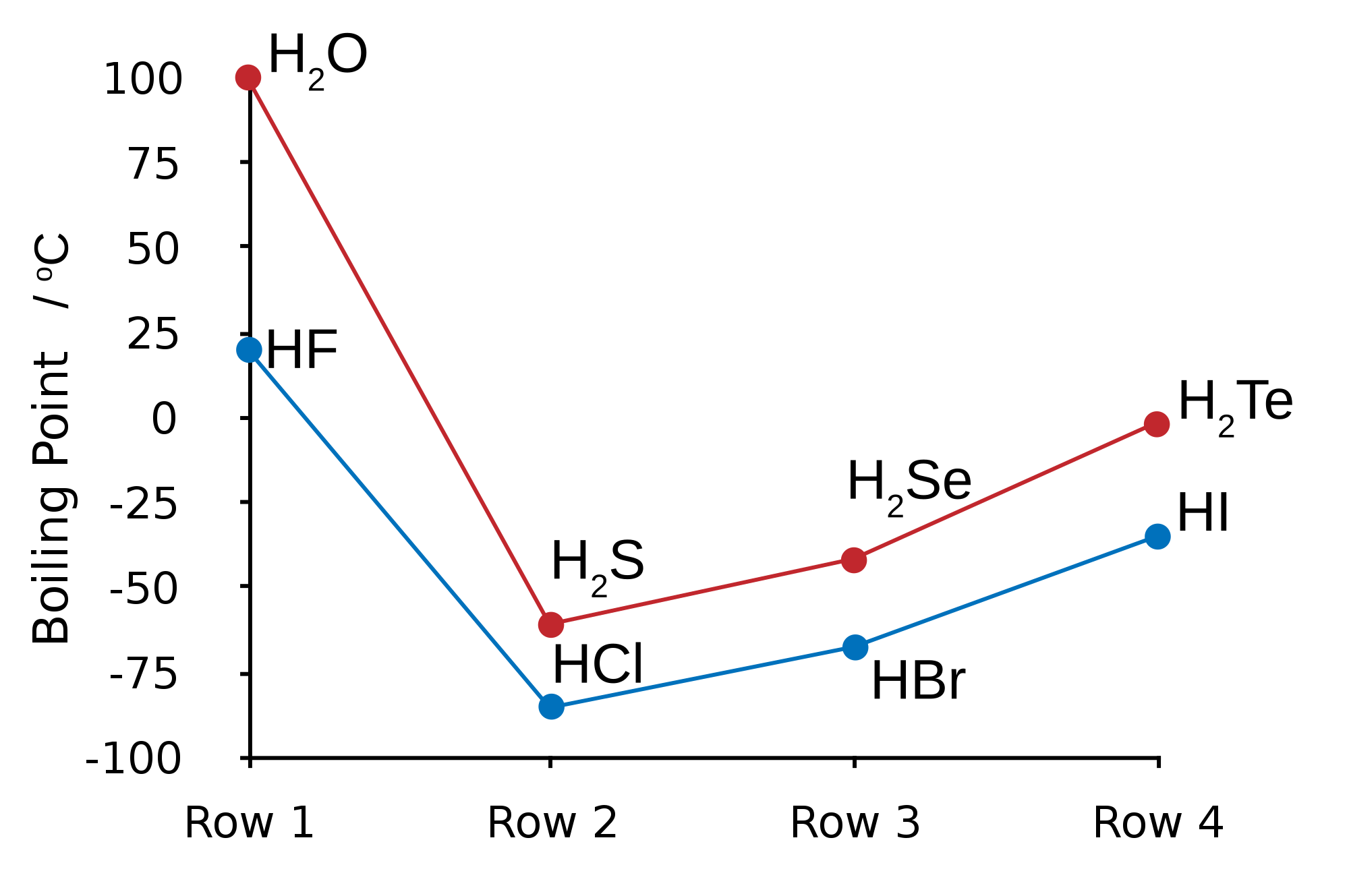
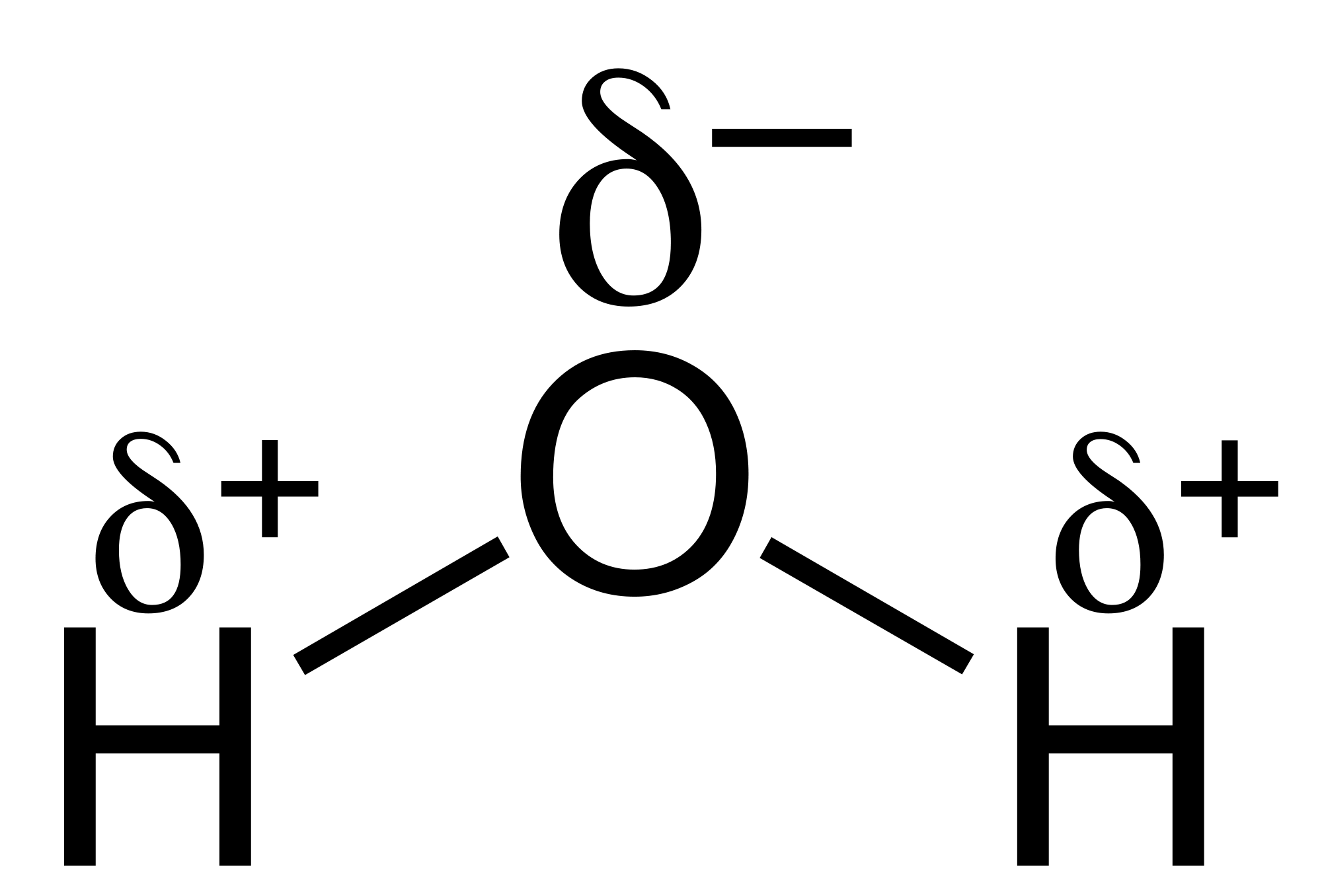
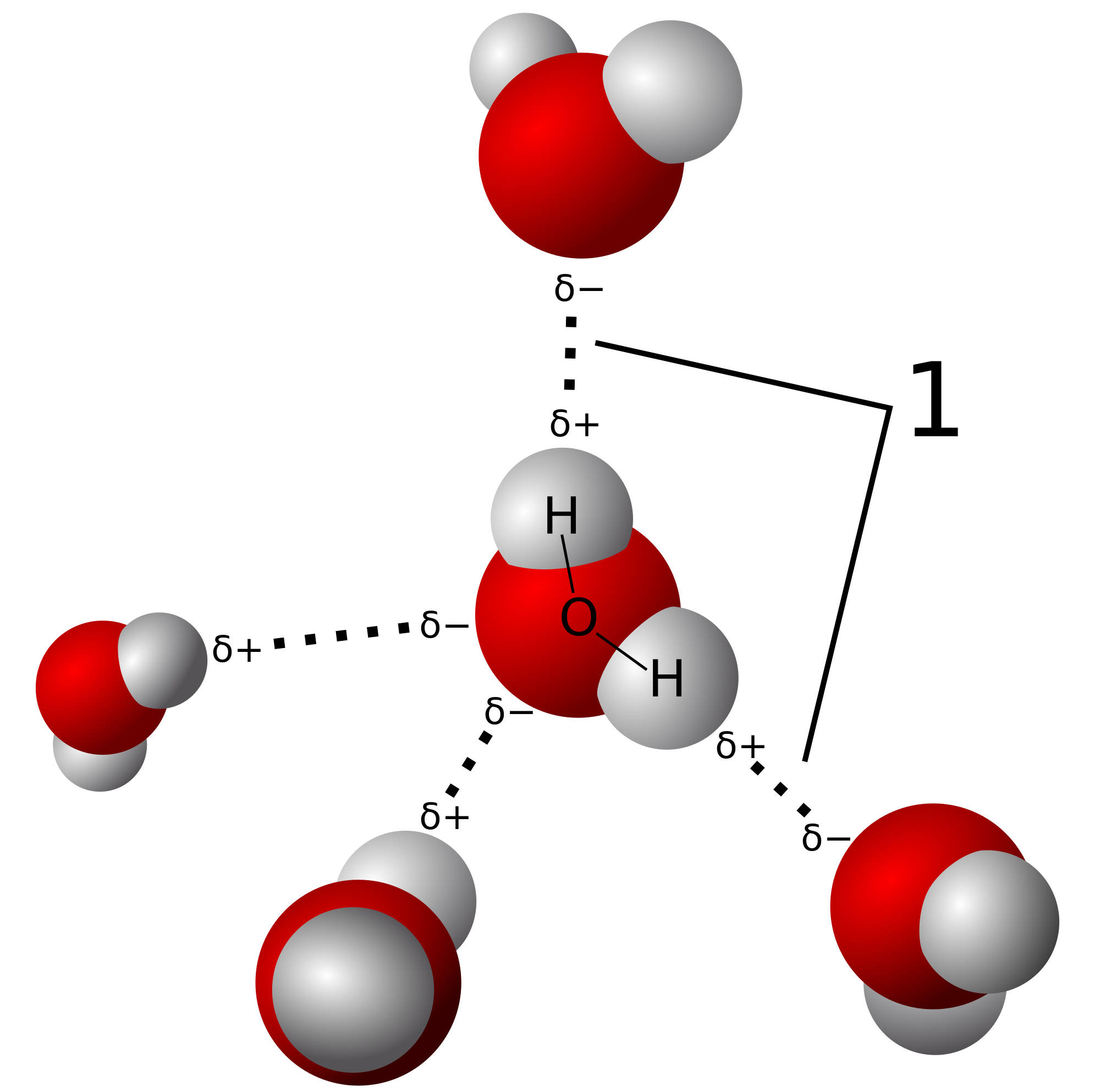
In the next part I'll go into more basic molecules of the heteronuclear diatomic type, such as hydrogen fluoride, HF.

11 Mar 2017

Chemical Wonders: Experimental Techniques (Part 6) - X-Ray Diffraction

The X-Ray and the Structure of Molecules

X-Ray diffraction is responsible for for some of the most important discoveries of the 20th century, from determining the structure of DNA, to the intricate carbon lattices of diamonds and graphite. The technique has developed over the years to cover more than just molecular solids, non-molecular solids and gaseous molecules. Modern techniques are capable of revealing information of polymers, proteins and other macromolecules.

There are several types of diffraction methods:

The two most common X-ray methods being powder x-ray diffraction and single crystal diffraction.
Electron diffraction is a method used for the elucidation of gaseous molecules and studying solid surfaces, Neutron diffraction is also another method used for diffracting lighter atoms such as A,D, and Li and distinguishing atoms with similar atomic numbers (not covering these).

What is X-ray diffraction?

X-rays exist in the wavelength of 10-10 m, or about 100 pm - which is approximately the same order of distances between molecules. This, in turn, means x-rays interact electrons present between molecules in a crystalline solid. These interactions are capable of producing high-resolution images of the structure of crystalline solids (or polycrystalline, i.e. DNA).

Here's an example of an x-ray diffractometer:

An X-ray diffractometer consists of: an x-ray source, a mount for the sample, a turntable, allowing you to adjust the angle of the sample in regards to the x-ray beam and the detector. Modern diffractometers, make use of imaging plate detectors, or charge coupled devices (CCD) area detectors. These components convert x-rays into light before recording the data, which allows for faster data collection. There are pixel detectors being researched, which will enable data collection to become more efficient by skipping the light-conversion step and instead measuring the radiation directly.

Diffractometers make use of the fact that the x-rays are scattered by the electrons orbiting nuclei and hence, the scattering power of nuclei is dependent on the number of electrons present in the system. The variable electron densities allow us to distinguish different types of atoms present in a sample. Using the X-ray diffraction method, being able to detect light atoms such as H bonded to heavier atoms is difficult, if not impossible because of the electron densities. Neutron diffraction is used for that purpose.

The Bragg Equation

If we take say, a crystal lattice and the atoms are in the form of the black dots (above), which are arranged into lattice planes (two). Now consider two waves (dotted lines), each of which are reflected by one of the lattice planes. These waves which are scattered (reflected) will only be in phase if the second wave is equal to the multiple (n) of the wavelength (𝜆). The spacing of the lattice also plays an important role (how far apart the lattice planes are from each other), which is represented by d. Using trigonometry, it can be deduced that the distance travelled by the second wave will be 2d x sin 𝜃. This relationship leads to Bragg's equation:

2d x sin 𝜃 = n𝜆

Before the waves are scattered they are in phase, so in order to remain in phase as they are scattered, the equation above must hold.

Check the links below for some more interesting info about this technique.

I'll update this post with some more images relating to simple diffraction patterns.

Thanks for reading!

Furtherther Reading:

Reference image in header (background):

https://commons.wikimedia.org/wiki/File:Zn-Mg-HoDiffraction.JPG

3 Mar 2017

Chemical Wonders: Experimental Techniques (Part 5) - Electron Paramagnetic Resonance

Using the power of the microwave

What is EPR (also called electron spin resonance, ESR) spectroscopy?

EPR spectroscopy utilizes the quantum nature of electrons by exciting them with microwaves, doing so creates a transition between the magnetic energy levels of electrons changing the 'spin' and angular momentum of the electron. This is called the Zeeman electronic effect, see below:

The spin 'up' and 'down' states are also given the 𝜶 and 𝜷 notations, respectively. 𝛥E corresponds to a microwave region in the microwave region in the electromagnetic spectrum, which is applied to the analyte, allowing two spin states to occur. The EPR spectrometer records these transitions and represents them in an EPR spectra. Compare this to NMR spectroscopy - which uses the nuclear 'spin' transitions as a result of blasting different radiofrequencies at the analyte using a magnetic field.

Typical EPR spectrometers operate at the 9-10 GHz range, otherwise known as the 'X-band' range. There are other bands used, however:

'L-band' : 1-2 GHz
'S-band' : 2-4 GHz
'Q-band' : 35 GHz
'W-band' : 95 GHz

More modern machines, such as the FT-EPR spectrometers are capable of much higher resolution spectra, which has allowed us to explore even more types of chemical species, such as the paramagnetic center found in a metalloprotein (like methemoglobin). I'll just drop in an interesting article where the blood (ionized by radiation) of Chernobyl workers were analysed using EPR spectrometry, here.

The EPR spectra

The EPR spectra is recorded in the form of the derivative of the very first peak in the spectra (see above). Why? This is because this form is more sensitive to the microwave signal, improving the signal : noise ratio, On the spectra, the absorption maximum is where the derivative is equal to zero - this is also the point where the magnetic sample B_sample is recorded. We find the g-value of the sample using the following equation:

𝛥E = hv = g_sample x 𝜇B x B_sample

The g-value, is calculated experimentally as the frequency of the wave v, is precisely known in modern spectrometers and h being the Planck constant, and 𝜇B being the Bohr magneton (a constant). Older spectrometers must be calibrated based on g_sample and comparing it with B_sample. g-values provide diagnostic information about the analyte you are investigating. Paramagnetic metal centres, for instance, the g-value is characteristic of the oxidation state, coordination numbers and even the symmetry of the molecule. System with cubic symmetry (T_d, O_h, and I_h) on the other hand, the g-value will depend on the principle axis when applied to the magnetic field. Samples are placed in magnetic fields on three orthogonal planes.

For example, Anisotropic systems with axial symmetry have two axis (x,y) which are different from a principal axis (z). This results in two g-value, g_⊥ (perpendicular from the principle axis) and g∥ (parallel to the principle axis). How does this relate to the symmetry? Well: g_xy = g_xx = g_∥, while, g_zz = g_⊥. These values only arise depending on whether or not the molecular principle axis is aligned with the magnetic field or not. Other anisotropic systems, where the x, y, z values are unique, consequently giving rise to three g-values: g_zz, g_xx and g_yy.
Isotropic systems on the other hand, such as a metal complex with 6 ligands (MX₆ species,O_h symmetry), are a bit simpler, as the three g-values that arise all equal each other: gxx = gyy = gzz = giso. This is because these molecules are perfectly symmetrical.

I'm unable to show these types of symmetry in EPR, however, this source from the University of Manchester provides a good visual of the spectra produced from isotropic and anisotropic systems outlined above.

Some examples of spectra:

Other information from EPR spectra include the nuclear spin quantum number (I), which is close to the paramagnetic centers (which is what EPR highlights). Where I =/= 0, the free electrons present in the paramagnetic species interact magnetically with the nuclei, causing a hyperfine interaction.This leads to further splitting in the Zeeman electronic effect, increasing the energy differences between spin states. However, this results in far more complicated spectra than shown above.

Of course, this is just an extremely brief overview of EPR spectra - however, this type of spectroscopy has wide applications from inorganic chemistry, identifying compounds in organic chemistry. It even has applications in biochemical systems, such as metal complexes found in proteins (Cu²⁺, Fe²⁺ etc.).

2 Mar 2017

What makes water so special?

Water is essential for life. Why?

Water is so normal for many of us, and we don't question why it is an essential part of life. Around 71 percent of our planet's surface is water, from the vast salt-water seas, the streams that flow from mountains and into lakes and to the frigid polar ice caps. It is also abundant in the universe, comprising of the most abundant elements: hydrogen and oxygen. It has been detected all across the milky way. In fact there is a "cloud" of water with over 140 million times the water on earth surrounding an area around a black hole called a quasar, 12 billion light years from here.

About everywhere water exists on earth, life does too. The answer lies in its chemistry - from its physical properties to how it interacts with the stuff around it

The physical properties of water

Water exists on earth in three main states: solid (ice), liquid, and gas (clouds). Water is most useful to life in liquid form at standard temperatures (25℃) and normal atmospheric pressure (1 atm). Water is also able to exist as a liquid at a broad range of temperatures, from 0℃ to 100℃ and compared to other similar compounds its boiling point is much much higher. See below:

Its solid state is also different from similar compounds: it is less dense than the liquid form, which is something almost unique to water. For example, liquid water's max density is 1,000 kg/m3 and solid water has a density of 917 kg/m3. Water expands in its solid state by about 9% compared to its liquid form.

Why does water have these properties?

Water, Hydrogen bonding and its importance to life

Water is what we call a polar molecule, one part of the molecule is much more negatively charged than other parts of the molecule. What this forms is an electrical dipole moment, which is the separation of more negatively charged parts of a molecule, see the diagram below:

It is the separation of slight negative and positive charge that gives water its special properties. The more negative areas attract the positive areas of other molecules, when this occurs a weak bond between the water molecules form. Up to four of these "hydrogen bonds" can be formed (two on the oxygen as it has two lone pairs of electrons),

These bonds are individually quite weak and are easily broken, but in large quantities has a dramatic effect on the substance's boiling and melting points, as well as the structural properties in solid form. As discussed above, ice is more dense and expands up to 9% more than the maximum density of liquid water. This is because the orientation of hydrogen bonds in water causes the molecules in solid form to push further apart which reduces the density of the solid. Below, "1" shows where hydrogen bonds occur.

Water's polarity also enables it to dissolve other polar substances, and enables an environment for many organic compounds to react with each other, that would otherwise be impossible in solid form and quite difficult in gaseous form. Hydrogen bonding isn't just found in water present in lifeforms, but also in many organic compounds such as DNA and every protein in your body. These compounds could only exist in your body in aqueous form (mixed with water) because of water's properties as a solvent.

Water is also involved in many biological reactions in many of which occur in metabolic pathways. In anabolic pathways, water is a product of forming large and complex molecules. While in catabolic pathways, water is always one of the reactants, that "add water" to the large molecules, breaking it down.

It is also an important to the pH balance of life forms, as the hydrogen ion (H+, a proton) acts as a "Lewis acid," which donates itself to a "Lewis base," often a hydroxide ion (-OH) to form water. It is this interaction (with other acids and bases too) that has enabled us to create the pH scale, which determines the concentrations of H+ ions and -OH ions present in a solution.

The many uses of water

Water has its many uses for us humans, besides for drinking. We use it in our agricultural industries, for cleaning ourselves, moving around the world, to generate power, to extinguish fires and, to have fun and relax in. It is even used to exchange heat because of its high capacity of heat absorption. This capacity, especially for vaporization (into gaseous form), is called the enthalpy of vaporization, which is the required heat needed to convert a quantity of substance into vapor form. This capacity makes it useful in many power stations, nuclear power plants or in old machine guns (like the Vickers machine gun). Its usefulness outside of needing it to stay hydrated makes it one of the most versatile chemicals in the universe.

Scientifically, it plays another role for us chemists. Namely, we use it to base many standards of measurement. This includes the degrees Kelvin (K), in which the base of the measurement was the triple point of water (0.01 ℃), in which water can exist as a solid, liquid or gaseous form at the same temperature. This point of measurement is exactly 273.16 K and is what we call and absolute temperature scale, this unit of measurement is used quite often in scientific equations. The measurement of degrees Celsius on the other hand relies on the melting point (0 ℃) and the boiling point of water (100 ℃). These units of measurement have been instrumental in experimentation and improving the reproducibility of experiments because units exist in easily replicated conditions.

. . .

Water is an interesting molecule - it doesn't fit in with molecules of similar size and type, which makes it have all sorts of interesting properties not found in the same way in other molecules. It is the most important molecules that has enabled life here on earth to exist the way it does. Without it, it'd be hard to say we'd be here at all.

Thanks for reading!

You can also check this same post out on minds, right here.

Don't forget to check out my Patreon, if you like the content I'm putting out:

https://www.patreon.com/MrElement

27 Feb 2017

"Green Chemistry" - Moving toward a sustainable future

Protecting our environment...with chemistry

Green chemistry, as defined by the EPA, is: "the design of chemical products and processes that reduce or eliminate the generation of hazardous substances." This type of research is at the forefront of developing sustainable technologies. Some of the goals of green chemistry include:

Using new solvents to replace volatile and hazardous substances, such as chlorinated and volatile organic substances.
Reducing the energy consumption in commercial and industrial processes; as well as reducing the amount of hazardous waste produced in industries.
Using renewable feedstocks, which is biological matter that can be used directly as a fuel. Or it can be converted into another fuel. Also called biomass feedstocks.
And using less hazardous chemicals in industrial processes.

At the beginning of this century, the journal Green Chemistry, published by the Royal Society of Chemistry provides a forum for developments in green chemistry. In the US, the American Chemistry Society Green Chemistry Institute (ACS Green Chemistry Institute) was established in order to promote the ideas and benefits green chemistry and "green engineering" to industries and the global chemical enterprise.

The challenges of building a sustainable future

The development of "green chemistry" techniques has been largely modeled after studies conducted in the late 20th century. Namely, Anastas and Warner (1998) developed principles of green chemistry, which can be summarized in 12 points:

Wherever it is practical to do so, synthetic methods should be used to ensure that the products of the method possess little or no toxicity to humans or the environment.
The synthetic methods should be designed in a way that maximizes the total amount of reactants used in the process to produce a final product. Ensuring very little goes to waste.
The products should preferably have reduced toxicity while keeping the efficacy of function of the replaced substance.
It is preferable to prevent waste before it is formed, as opposed to treating or cleaning it after it is formed.
"Auxiliary substances" such as solvents and separating agents should be used only when necessary or preferably are innocuous (harmless) when used.
Feedstock used for energy production should preferably be renewable whenever economically viable rather than depleting feedstocks.
Whenever feasible, synthetic methods should be done at ambient temperatures and pressures. The environmental and economic impacts (in the long and short term) of energy requirements should be recognized.
Unnecessary protection, deprotection steps or any derivatisation in the synthetic method should be minimized or completely avoided in organic synthesis.
Catalysts, as opposed to stoichiometric reagents are far superior for chemical synthesis. And, wherever possible, the catalysts should be as selective as possible.
Chemical products should not persist in the environment after their function has come to an end. Instead, they should degrade into innocuous products or be reused in some other process.
Substances used in chemical synthesis should be chosen as such that they reduce chemical accidents such as explosions, and fires.
Further developing analytical methods that allow real-time monitoring and control during a process as to predict and minimize the formation of potentially hazardous substances.

With those 12 principles in mind and developments in other fields, it's possible to build a better future. In fact, the Presidential Green Chemistry Challenge Awards was established in 1995 to challenge chemists and encourage the development of green technologies at the academic and commercial levels. You can find a list of all years' winners since then here.

24 Feb 2017

Chemical Wonders: Experimental Techniques (Part 4) - Nuclear Magnetic Resonance

Nuclear Magnetic Resonance Spectroscopy

Note: Assumed knowledge or previous experience with NMR in High School or University.

This is perhaps one of the most important tools of chemistry, which involves an analyte absorbing energies from radiofrequencies. In particular, the absorption of radiofrequencies, is affected by the magnetic environment of the atomic nuclei in compounds. Thus it allows us to deduce structural information on the compound in question. It is typically used to determine the relative chemical environments of active atomic nuclei present in a compound, usually we analyse a solution of our analyte. Using a solution, we are also able to investigate the chemical behavior of the analyte.

We can take advantage of many different types of spectra depending on the atomic nuclei we want to analyse in a compound, the most commonly recorded spectra belongs to the Carbon-13 nuclei, in ¹³C NMR, usually used by organic chemists.

Suitable Nuclei

The three isotopes of hydrogen each have their own nuclei, which give their own NMR spectra.
From left: Hydrogen, Deuterium and Tritium. Wikimedia source.

All nuclei have a property called "nuclear spin," a quantized property which is described by the spin quantum number, I, with the corresponding numbers 0, 1/2, 1, 3/2, 5/2 and so on. When nuclei aren't exposed to a magnetic field, the spin states are considered degenerate, i.e. the spin states have all the same energy. Conversely, when a magnetic field is applied to a nuclei, it becomes "split," i.e. it becomes non-degenerate, and the spin states have different energy levels. Nuclei where the value of I, is equal to 0, they are said to be NMR inactive. On the other hand, for nuclei where I = 1/2, the nuclei is said to be NMR active, examples include ¹H and ¹²C nuclei.

The ¹³C NMR spectra is important, because the carbon-13 isotope has a relative natural abundance of 1.1 %, so when investigating a compound, only 1% of all carbon atoms present in the compound will be the isotope. As a result, the relationship between ¹H - ¹³C coupling has a consequence on the observed NMR spectra.

Given all of this, what constitutes a suitable nuclei? And what are some important factors that determine when an NMR spectra will be observed?

The nuclear spin quantum number needs to be I ≥ 1/2;
In general, it is advantageous for the particular nucleus to be in relative abundance, the ¹³C isotope is one exception, though. Abundance of a particular isotope (isotopic enrichment) can be utilized to enhance the signal : noise ratios;
The nucleus must posses a relatively short spin-relaxation time (T₁, given in seconds), which is dependent on the properties of the molecular environment and the nucleus itself;
Finally, if I > 1/2, it results in a non-spherical distribution of nuclear charge, which is termed a quadrupole moment. This leads to relatively short values and causes the signals associated with the quadrupole moment to appear broad; signal broadening is also observed on nuclei attached to the nuclei that possesses a quadrupole moment. For example, ¹¹B as well as an ¹H NMR spectra of protons attached to ¹¹B.

The importance of the T₁value becomes apparent when observing elements that have more than one NMR active form, for example ⁶Li and ⁷Li are both NMR active, but their values are different. Typically, ⁷Li has T₁< 3 s, while for ⁶Li is T₁ ≈ 10 to 80 s. Considering the relative abundance of these isotopes, we find that ⁷Li has an abundance of 92.5%, which makes it more suitable than ⁶Li .

Chemical Shifts and Resonance Frequencies

You can read a table of frequencies at which you would be able to observe certain nuclei using NMR here. NMR spectrometers are calibrated to particular resonance frequencies which are specific to a nucleus (e.g. ¹H, ¹³C, ¹¹B, ³⁵Cl, ³⁷Cl absorb different radiofrequencies), for example a 400 MHz spectrometer set to 400 MHz, you will only be able to observe ¹H nuclei; using the same 400 MHz spectrometer, but calibrated to 162 MHz, you would only be able to observe ³¹P.

¹H NMR experiments involve identifying protons that are in different chemical environments (i.e. a H is bonded to different groups/atoms), which resonate at different frequencies.

For example, the proton NMR spectra of benzene (C6H6) only appears to have
one peak. Why? Every ¹H nuclei is bonded to the same 'environment' of a
C=C bonded to another proton.

The same is true for other types of NMR, which each give their own characteristic signals. Signals in an NMR spectrum are given a chemical shift value, 𝛿, which is relative to the specific radiofrequency of that nuclei. The chemical shift value is a parameter that is independent from the magnetic field applied to the analyte. It can be defined as:

𝛿 = (v - v₀) / v₀= Δv / v₀

The value of 𝛿 is usually quite small and inconvenient, so we usually multiply by 10⁶, converting it into ppm (parts per million). The IUPAC convention for 𝛿, according to their Gold Book is defined as:

𝛿 = (v - v₀) in Hz / v₀ in MHz

For ¹H and ¹³C NMR, the standard reference is tetramethylsilane, SiMe4. It is used as a reference for the shift, so to speak, of the signals from a particular nuclei from the reference signal. A positive 𝛿 is a shift to a higher frequency, while a negative shift (or less positive), means there is a shift to a lower frequency. This difference is the chemical shift.

Homonuclear spin-spin coupling

A nucleus can only occupy two spin states (-1/2 and +1/2), the energy difference between these spin states is dependent on the magnetic field produced by the NMR spectrometer. If say, there is a system where there are two magnetically non-equivalent ¹H nuclei, there can only be situations (H_A and H_B) that can arise when a magnetic field is applied:

The NMR signal for H_A is split into two equal lines when a magnetic field is applied to H_B, these equal lines are also produced by H_B. The lines produced by are dependent on the which spin state of is "seen" by the spectrometer. These protons are said have coupled, producing two "doublets." The coupling constant, J, which is measured in Hz is defined as the splitting that occurs between two lines in each doublet.
When no coupling of nuclei occurs. The local magnetic field produced by the spin of results in two resonances, each of these a singlet, as no coupling has occurred between the two nuclei.

Heteronuclear spin-spin coupling

Statistically, the ¹³C nuclei is quite rare. So in ¹H NMR of say, acetone and assuming a natural distribution of carbon isotopes, you will not be able to observe the coupling of ¹H - ¹³C. Conversely, You will observe this coupling when using ¹³C NMR spectrum on acetone, and will only observe a singlet because of the C=O group, and a quartet because of the two chemically equivalent -CH3 groups. You can see this in this spectra here.

Ion-solution exchanges can be observed using NMR

The exchange of cations into solution occurs at slow enough speeds to be observed at the NMR spectroscopic timescale. We utilize the ¹⁷O isotope as a label: because it is NMR active, and because I = 5/2. From the signal ratio of ¹⁷O present in a naturally isotopic distribution of co-ordinated water (recall H₂O can form weak bonds with ions), you can actually find the hydration value of a given ion-water complex. For example, the Cu2+ ion has been found to co-ordinate (bond) with six water molecules, forming the complex ion [Cu(OH₂)]²⁺ (hexaaquacopper(II)), forming an octahedral complex. See model below:

Hexaaquacopper(II), has six water molecules whose
hydration number using ¹⁷O can be observed.

Another exchange process are redistribution reactions, in which, substituents (chemical groups) are exchanged between chemical species - but - the types of bonds and number of bonds remain. Similar to a substitution reaction. For example, the reaction of Triethyl phosphite and Phosphorus trichloride:

PCl₃ + P(OEt)₃ ⇌ PCl₂(OEt) + PCl(OEt)₂

We can find were the equilibrium lies using ³¹P spectroscopy, and the rate data by analysing the variation in the signal integrals (peaks), conversely, you can find the equilibrium constant (Kc) when no more variation is found in the signal integrals. Finding the equilibrium will allow you to find the all-important free energy change of the system (ΔG^o = -RT ln K). Using this relationship you can then find the at varying temperatures using ΔG^o = ΔH^o - TΔS^o. Thus, we can find the equilibrium position can be found in relation to temperature (remembering that ΔH^ois almost 0, using the second law of thermodynamics), we can then differentiate to eventually find:

d ln K / dT = ΔH^o/RT²

I won't go into how NMR machines work, but here's what they look like:

A Bruker NMR spectrometer connected
to a computer. Wikimedia link.

A high-powered NMR machine from Varian, capable of
using 900 MHz frequencies.

23 Feb 2017

Unwinding the Double Helix: The Structure and Function of Nucleic Acids (Part 3)

The Function of Nucleic Acids

So far, I've only discussed the main structures of nucleic acids - the primary, secondary and tertiary structures. This section will focus on the function nucleic acids in cells and the denaturation of nucleic acids.

Genetic Biochemistry - from genes to proteins

In my blogs I haven't quit covered the biochemistry of genetics in detail, so think of this part as a (very) brief overview of molecular genetics. It's important to remember that the main function of nucleic acids is to store genetic information and that they are the key to biochemical processes, namely, protein synthesis.

What's in a genome?

All living things carry genes - sections of DNA which, when 'read' by your molecular machinery, result in the expression of a particular gene. Expression leads to the synthesis of a chemical, usually a protein of some description, such as an enzyme. Depending on the organism, their genetic information can be stored as double-stranded DNA or RNA molecules which can vary in length. Genomes are also present in viruses (which aren't considered 'alive'), which generally contain a few thousand bases (b) that code for the proteins that make up the viral structure.

The E. coli bacteria had its circular genome sequenced in 1997, which contains about 4.64 million base pairs (1.6 mm in theoretical length), all of code for about 4000 genes, 50 of which are considered 'non-essential'. Another bacteria, the pathogenic Clostridium difficile has about 4.4 million base pairs. An interesting thing to not about these bacteria is that, even though they contain less genetic material than us, they have a higher gene density than us.

Comparatively, the human genome was sequenced in 2001, we found out that it contains about 3.0 ×10⁹ base pairs (3,200 Mb, megabase pairs). The full sequencing and analysis of our genome revealed that:

There appear to be about 30,000–40,000 protein-coding genes in the human genome—only about twice as many as in worm or fly.

This came as a surprise to many who had thought that we were more complex than other organisms, and the fact that only 1.33x10-5 % of our genome codes for essential proteins. Much of our genome has been termed as 'junk DNA.' It is possible that this junk, referred to as non-coding DNA (ncDNA), is essential for regulation at the genetic level. I'll leave some links at the bottom of this post if you want to read more about this section of our DNA.

Gene Expression: An overview

In most organisms it is those genes that are 'read,' synthesising RNA for use by ribosomes, and thus directing the synthesis of proteins. This process of gene to protein is called gene expression.

Transcription: the first step of gene expression

The first step involves the DNA strand being unwound, by a leading enzyme. Behind it is RNA polymerase, along with other enzymes, which begins to 'read' the DNA strand, which becomes the template for the RNA being produced. It works in a similar fashion to DNA replication, but instead produces a single-stranded RNA molecule, called mRNA. This process is powered by ribonucleoside triphosphates, such as: ATP, GTP, CTP, and UTP, which are all needed to make RNA. Again, similar to to DNA replication, this process requires the use of a class of enzyme called polymerases. Specifically, the RNA polymerases. This process can be summarised below:

1) RNA polymerase bind to the promoter, which begins transcription

2) RNA polymerase goes along the DNA strand, opening up the strand "downstream," while the strand closes "upstream." A strand of RNA is produced which is complementary to the bases present on the template strand:

3) Once RNA polymerase reaches the termination "STOP" codon, it detaches from the DNA strand and a pre-mRNA strand is produced. This is then 'edited' by enzymes, removing non-essential regions called introns (I'm not going to cover this process here).

Translation: proteins from mRNA

mRNA exits the nucleus of a eukaryotic cell via nuclear pores, it then comes into contact with a special protein called a ribosome. Ribosomes work together with strands of RNA called tRNA, which have 3 bases (a anti-codon) which are complementary to the codons present in mRNA. tRNAs basically are your cell's code-cracking sheets, as they are attached to the amino acid which correspond to the mRNA codon. The ribosome is effectively the machinery that sticks together the amino acids on the tRNA, eventually creating a protein. Proteins aren't usually folded by themselves, and often require assistance via a molecular "chaperone," a family of proteins called chaperonins. There are 64 combinations of codons, all of which correspond to an amino acid, found on tRNA. Here is a table:

Nucleic Acid Denaturation

As mentioned previously, DNA and RNA is incredibly stable - however, because of the need to replicate DNA for meiosis and mitotic cell division, the secondary structure must not be too stable. If DNA and RNA where to be too stable, replication and gene expression rely on the uncoiling, and recoiling of double-stranded nucleic acids. Physiological conditions (~pH = 7, 298.15 K (25 ℃), 1 atm) allow cells to be opened up by the required enzymes in vivo.

But what happens if a nucleic acid's secondary structure opens up too much? If the secondary structure is lost, it is called denaturation. Separating strands, like all things in chemistry, obey thermodynamic laws, in this case the free energy change:

ΔG = ΔH - TΔS (helix ⮂ random coil)

The secondary structure is stabilised by phosphodiester bonds, hydrogen bonds and base stacking, as mentioned in the previous sections. These interactions contribute to the heat of a nucleic acid system, i.e. they are enthalpic, so ΔH in the equation above will be positive. And since helices are very ordered, the entropy change, once denatured, will result in a positive ΔS.

Low temperatures result in a lower ΔG, because the - TΔS portion of the equation is positive, due to a reduction in randomness because of a lower temperature. This results in a ΔG > 0, meaning the helix is relatively more stable than at higher temperature. As such, when the temperature increases, - TΔS becomes greater than the ΔH value, resulting in ΔG < 0, which decreases the stability of the helix, eventually the double helix falls apart. It is possible that slowly cooling can reverse this process.

Denaturation of nucleic acids can actually be observed through a spectrometer set at the ultra-violet range (260 nm) when slowly heating a solution of DNA. When doing this, you would notice that the absorbance of the solution increases over time as the purine and pyrimidine structures become more "free." This happens because the structure of DNA, where nucleotides are packed in tightly in a double helix results in a decrease in light absorption, a process called hypochromism.

Futher reading on 'Junk-DNA' :

As always, thanks for reading!

Don't forget to check out my Patreon, if you like the content I'm putting out:

https://www.patreon.com/MrElement

Links provided bring you to some of the info I used, the first year university textbook, "Biochemistry: Concepts and Connections," 1ED, by D.R. Appling, Pearson Ed. LTD. Chapter 4: Nucleic Acids, pgs 126-129, was used as a guide to write this post. You can buy it here.

I also used the textbook, "Molecular Biology," 5ED, by Weaver, Robert F., McGraw HIll Publishing; which if you're interested (and have the money to spare). Chapter 3: An Introduction to Gene Function, pgs 31-45, was used as a guide to write this post. You can buy it here.